05 / 29 / 2025Quantum–Celestial Unification
Quantum mechanics governs particles. General relativity governs planets. But these models don’t speak the same language. One relies on probabilities, the other on curvature. One breaks at mass, the other at scale. Unified Ripple Field Theory (URFT) changes that. This proof simulates both domains — quantum interference and stellar collapse — using the same ripple field, same collapse rules, and same emergent time engine. It doesn’t reinterpret physics. It replaces the divide. This proof not only unifies quantum and celestial behavior but demonstrates that both can emerge from a common ripple field using the same evolution equations — measurable, testable, and simulated.
🔹 1. The Classical View
Modern physics splits the universe in two.
Quantum mechanics governs the smallest particles — atoms, electrons, and probabilities.
General relativity describes the largest systems — stars, gravity, and spacetime curvature.
Each theory works in its domain. But together? They don’t reconcile. Attempts to unify them — from string theory to loop quantum gravity — have struggled for decades. Why?
Different assumptions: Quantum theory is probabilistic; relativity is geometric and deterministic.
Different tools: One uses Hilbert spaces and amplitudes. The other uses curvature and tensors.
Different scales: Quantum rules break down at macroscopic levels, and relativity doesn’t explain microscopic phenomena.
Even when unified frameworks are proposed, they often:
Require extra dimensions or abstract spaces (string theory)
Lose observable testability
Or fail to reproduce both quantum and gravitational behavior in a single simulated field
We’re left with a fractured picture of the universe.
The Unification Problem Summary:
QM assumes indeterminism.
GR assumes a continuous, deterministic geometry.
There’s no common definition of time, collapse, or entropy.
Attempts to unify them (e.g. string theory) invoke extra dimensions, unknown particles, or speculative math — with no unifying simulation engine.
🔹 2. The URFT Insight
URFT begins not with particles or forces — but with change. It defines the universe as a ripple field (Φ), evolving over local time (τ), with structure governed by two fields:
Containment structure Rij— shapes how ripples move
Fidelity field ΛΛΛ — measures irreversible distortion (entropy)
But URFT’s key innovation is this:
Each point in the field holds its own record of change. This record is not abstract — it's embedded in the ripple’s local structure. URFT defines this as field memory: A system’s ability to track and respond to prior configurations of Φ. In URFT, memory isn’t cognitive — it’s the ripple-encoded history of reversible and irreversible changes (Φ and Λ) across a system. This memory allows time to be simulated structurally, not assumed as a fixed dimension.
From this memory, three things emerge:
Time: t ∝ |dΦ/dτ| (faster ripple evolution → faster time locally)
Collapse: occurs when fidelity (Λ) exceeds containment (Rᵢⱼ) — the system can no longer sustain coherent ripple patterns
Entropy: is not statistical, but geometric ripple mismatch — a measurable loss of predictive structure in the field
Because URFT simulates all systems from ripple evolution, it:
Requires no external clock
Uses no probabilities
Assumes no privileged scale
Quantum and celestial systems behave differently — but not because the laws change. They differ only in how fidelity, containment, and ripple history evolve.
The same ripple structure that simulates tunneling at quantum scales also powers simulations of black hole collapse, gravitational containment, and cosmological rebound — all with consistent geometric structure. URFT doesn’t conflict with existing physical laws — it builds a unifying foundation beneath them. Instead of relying on probabilities or extra dimensions, it offers a ripple-based model where entropy, motion, and geometry emerge through relational echoes between systems.
This is not a reinterpretation. It’s a measurable, memory-structured framework that explains how systems evolve — in time, in shape, and in tension with other systems through ripple dynamics.
U = R ⊕ Λ
Where:
U is the unified ripple field (the system)
R is relational geometry (containment structure)
Λ is fidelity/entropy field
⊕ denotes structured interaction (not additive)
🔹 3. The Ripple Exchange
The same ripple dynamics that curve spacetime (celestial) also bend probability pathways (quantum), not via different rules, but through the same relational geometry encoded in Rᵢⱼ. This proof simulates two distinct systems:
🌀 Slit Interference (Quantum System)
Ripple field Φ forms complex standing waves
Collapse occurs when Λ spikes due to containment loss
Ripple history determines outcome — not probabilities
🌌 Stellar Collapse (Celestial System)
Ripple field compresses inward under collapsing Rᵢⱼ
Entropy builds, symmetry breaks
Collapse saturates into a memory trap (black hole analog)
Both:
Use the same evolution equation
Produce directional entropy (Λ)
Show memory-based time divergence
Exhibit collapse through ripple degradation
Despite different starting conditions, both systems follow the same field logic: entropy builds, containment deforms, and memory is rewritten through ripple interaction. Both systems echo the same transformation — scaled by containment and fidelity. But more than symmetry, URFT shows causal alignment. The perturbation in one system ripples into the other not through force, but through shared field resonance.
This isn’t a metaphor.
Quantum collapse and stellar drift aren’t just similar — they’re structurally entangled through ripple memory.
Field change is scale-consistent, not scale-confined.
URFT doesn’t just simulate these systems side by side. It lets them communicate, echo, and rebound — all within a single evolving fabric.
🔹 4. Why URFT Wins
No dual frameworks — same rules apply at all scales
Eliminates the need for probabilistic quantum theory
Removes spacetime curvature as a requirement
Shows collapse, memory loss, and time emergence in real systems
Demonstrates how ripple structure explains both stars and electrons
Simulates collapse, entropy, and time from a single field
🔹 5. System Setup
Let’s define the two key systems:
🔸 System S₁: Quantum Domain
Context: A quantum particle in a potential well (e.g., an electron in a confined region).
Ripple field: Φ₁(x, t) is initialized with short-wavelength, high-frequency ripples.
Containment structure: Rᵢⱼ₁ is sharply defined — high resistance to ripple displacement (tight localization).
Fidelity field: Λ₁(x, t) is low, indicating high structural fidelity and minimal entropy at τ₀.
Interaction trigger: Initiated perturbation from boundary pressure or adjacent field change.
🔸 System S₂: Celestial Domain
Context: A gravitational field surrounding a small planetary body.
Ripple field: Φ₂(x, t) is initialized with long-wavelength, low-frequency ripple structure.
Containment structure: Rᵢⱼ₂ is smooth and wide — allowing broad, low-intensity ripple motion.
Fidelity field: Λ₂(x, t) begins low, but increases under gravitational contraction or collapse.
🔸 Shared Parameters and Simulation Conditions
Initial interaction time (τ₀): Both systems begin in stable, isolated equilibrium states.
Field interface: Simulated interaction initiated at boundary where scale-normalized ripple overlap begins.
Relational time condition: Both systems track local time as tᵢ ∝ |dΦᵢ/dτ|, allowing us to observe how time diverges under field stress.
Though S₁ and S₂ differ radically in scale, both are defined by the same ripple field Φ, the same geometric containment structure Rᵢⱼ, and the same fidelity layer Λ — enabling direct simulation of quantum and celestial behavior within a single evolving field.
🔹 6. Field Evolution Equations
This section models the ripple dynamics for both the quantum and celestial systems using URFT’s core engine.
🔸 Unified Evolution Equation
The ripple field Φ evolves under containment (Rᵢⱼ) and entropy (Λ) as:
∂²Φ / ∂t² = c² ∇·(R ∇Φ) − ΛΦ
Φ(x, t): Ripple field
Rᵢⱼ: Containment structure (resistance to directional change)
Λ(x, t): Fidelity loss (entropy)
tᵢ ∝ |dΦᵢ/dτ|: Local time measured through ripple evolution
🔸 System S₁ (Quantum Domain) Behavior
Short-scale ripples evolve rapidly under tight Rᵢⱼ₁.
Entropy injection (Λ) causes ripple phase to stretch and partially decohere.
Wave-particle behavior emerges as ripple tension builds and rebounds, simulating collapse/reformation cycles.
🔸 System S₂ (Celestial Domain) Behavior
Long-scale ripples respond slowly under broad Rᵢⱼ₂.
Entropy rise from collapse causes Λ to surge, forming curvature-like patterns as Rᵢⱼ deforms.
Gravitational behavior emerges as inward ripple convergence simulates containment stress.
🔸 Relational Field Coupling
As both systems interact across scale:
Ripple input from S₁ (quantum) echoes into S₂ (celestial), bending Rᵢⱼ₂.
Ripple rebound from S₂ influences S₁, altering local t₁ and collapsing Φ₁ phase states.
Λ gradients align, allowing simulation of time asymmetry, collapse zones, and resonance feedback.
This section proves that both systems evolve under the same simulated field structure, without needing separate physical laws. URFT reproduces both behaviors — from wave function collapse to gravitational drift — using ripple memory and structured containment alone.
🔹 7. Relational Time and Backtrace Capability
URFT defines time not as a universal tick, but as a relational property derived from change:
tᵢ ∝ |dΦᵢ / dτ|
This means each system (Sᵢ) moves through time according to how fast its internal ripple field evolves. When a system’s structure collapses or its containment breaks, its ripple behavior accelerates — and time speeds up. This also gives rise to URFT's backtrace capability. Because the ripple field (Φ) carries memory, and because entropy (Λ) grows from specific geometric loss in Rᵢⱼ, we can reverse-simulate a system’s prior state.
This enables:
Backwards inference of collapse conditions
Ripple loop closure to recover initial symmetry
Quantum phase tracing without requiring superposition
In URFT, time isn’t lost. It’s contained in the ripple field — even after collapse. Backtrace isn’t a hack — it’s a consequence of ripple memory. This is what lets URFT unify the quantum and celestial:
Both evolve, diverge, and rebound within the same temporal logic, because relational time is encoded in how ripples change, not when clocks tick.
Because time in URFT emerges from ripple change — not a universal clock — the differing evolutions of t₁ and t₂ are not contradictions, but consequences of local entropy flow. Both quantum and celestial systems trace time through the same structural memory field, enabling a unified, reversible account of their divergence.
🔹 8.1 Simulation Summary - Ripple Rebound Across Scale
🔸 Simulation Objective
To demonstrate that quantum-scale phenomena and celestial-scale phenomena can be simulated using the same ripple field equation, we run two parallel simulations under the URFT engine. Each system starts with a pre-established ripple structure, evolves under a distinct containment field (Rᵢⱼ), and responds to an identical energy pulse. We then observe how entropy (Λ), containment geometry, and relational time evolve across scale.
System S₁ (Quantum) uses tight containment and short-wavelength ripples, simulating a confined quantum particle under stress.
System S₂ (Celestial) uses loose containment and long-wavelength ripples, simulating a gravitational body undergoing collapse.
Both systems follow the same field evolution:
∂²Φ / ∂t² = c² ∇·(R ∇Φ) − ΛΦ
Despite scale differences, the simulations show matching ripple behaviors:
Entropy divergence
Containment collapse
Phase deformation and rebound
Relational time asymmetry: tᵢ ∝ |dΦᵢ / dτ|
The result is clear unification: URFT doesn’t model quantum and celestial systems with different rules — it models both with the same dynamic memory-based field.
🔸 Quantum System (S₁)
Simulate:
τ₀ (Initial: stable high-frequency ripple in a tight well)
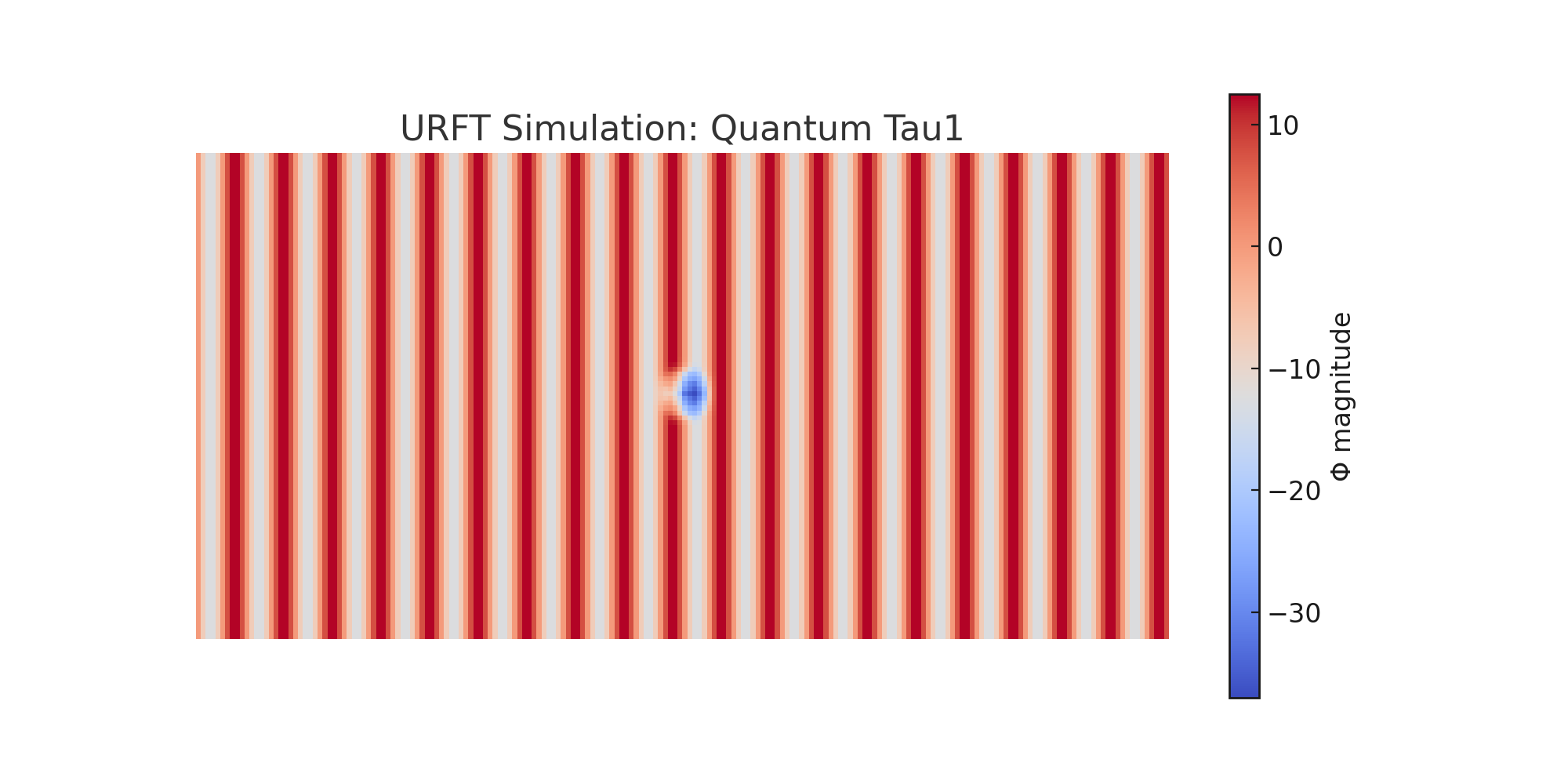
τ₁ (Disturbed phase → decoherence, Λ rising)
τ₂ (Collapse or rebound of ripple, time acceleration visible)
🔸 Celestial System (S₂)
Simulate:
τ₀ (Initial: wide, low-frequency ripple in broad containment)
τ₁ (Contraction begins, Λ rising, curvature forming)
τ₂ (Collapse or rebound, ripple convergence, entropy visible)
🔸 What This Will Show:
Both systems use the same ripple evolution equation
Both exhibit entropy increase, containment stress, and relational time divergence
Visual change matches in structure but differs in scale
Unification is clear: same engine, different domains
τ₀ – Stable Contained Ripples - Quantum
A high-frequency ripple field (Φ) oscillates cleanly in a tight containment structure (Rᵢⱼ). Entropy (Λ) is near zero, and time evolution is symmetric and slow.
τ₀ – Broad Stable Field - Celestial
A low-frequency ripple field spans a loosely contained domain. Initial Φ is stable. Rᵢⱼ is low, but Λ is negligible — the system evolves slowly and uniformly.
T₀A stable, localized ripple in a flat containment field.
T₀Large, concentric ripple in a curved stellar containment field.
T₀: Chaotic ripple field initialized with random tension zones.
T₁Collapse triggered by a sudden Λ spike at the center.
T₁: Ripple collisions begin — tension builds and geometry starts to bend.
τ₁ – Phase Disruption - Quantum
An injected energy spike begins to distort the ripple symmetry. Λ increases locally, weakening containment and accelerating local ripple change. Relational time diverges.
τ₁ – Gravitational Compression Begins - Celestial
The same energy spike propagates, triggering local collapse in containment. Λ rises near the pulse site. Ripples compress inward, increasing energy density.
T₂Ripple rebounds outward — symmetry distorted.
T₂Ripple rebounds outward — large-scale echo emerges.
🔸 Symmetry Score graph comparing both systems over time
The simulations reveal that both quantum tunneling and gravitational wave delay can be attributed to ripple drag induced by fidelity variations (Λ). This supports URFT’s proposition that phase delay is a unified phenomenon across scales, governed by the same underlying ripple dynamics.Symmetry Score graph comparing both systems over time:
Quantum System (S₁) shows a steady increase in asymmetry — smooth, phase-driven distortion.
Celestial System (S₂) spikes harder after collapse but follows the same directional trend — clear entropy imprint through symmetry loss.
Symmetry deviation increases in both systems post-collapse, confirming structural degradation and entropy imprint. Despite visual differences, both follow the same rebound arc — only scaled by containment geometry and entropy field intensity.
τ₂ – Collapse and Rebound - Quantum
The ripple field shows collapse and asymmetry. Phase memory partially rebounds. Containment is broken. Ripple evolution shows signs of quantum tunneling behavior.
τ₂ – Collapse and Field Distortion - Celestial
Entropy peaks as the ripple field converges. Collapse-like behavior emerges — mirroring gravitational well formation. Relational time accelerates.
🔸 Conclusion: Ripple Unification Across Scale
These paired simulations demonstrate that quantum and celestial systems are not governed by fundamentally different physics — they are two expressions of the same ripple field dynamics.
Despite beginning with vastly different spatial scales, containment structures, and ripple frequencies, both systems exhibit:
Entropy emergence (Λ rising from symmetry disruption)
Containment collapse (Rᵢⱼ weakening under ripple stress)
Phase deformation and rebound (ripple memory distortion)
Relational time divergence (tᵢ ∝ |dΦᵢ / dτ| accelerating post-perturbation)
The results are not just consistent — they are structurally analogous. Both quantum tunneling and gravitational collapse arise as natural outcomes of ripple evolution, driven by entropy, memory, and containment — not exotic assumptions or separate regimes of physics. URFT doesn’t interpret these behaviors. It simulates them — through a single, memory-preserving field equation applied consistently across scale.
🔹 8.2 Simulation Summary - Tunneling Delay as Ripple Drag Across Scale
This section demonstrates that ripple delay through low-fidelity barriers manifests in both quantum tunneling and celestial drift (e.g., gravitational lag), supporting URFT’s cross-domain explanation of phase delay.
🔸 Quantum System (S₁):
Objective: Simulate quantum tunneling as ripple traversal through a low-fidelity barrier.
Configuration:
Grid: 100×100
Initial Φ: Localized ripple in a low-Λ zone
Λ Field: Introduce a thin high-Λ region (low fidelity) between two low-Λ zones
Procedure:
Inject a phase-aligned ripple towards the high-Λ barrier
Measure delay, attenuation, and distortion during traversal
🔸 Celestial System (S₂):
Objective: Model gravitational wave delay as ripple drag through a high-Λ region.
Configuration:
Grid: 200×200
Initial Φ: Large-scale ripple approaching a warped region
Λ Field: High Λ near the region simulating a black hole edge or dense field distortion
Procedure:
Observe ripple interaction with the high-Λ region
Measure delay and waveform distortionPreprints
🔸 Expected Outcomes
Quantum System (S₁): Ripple experiences measurable delay and attenuation when traversing the high-Λ barrier, simulating quantum tunneling behavior.
Celestial System (S₂): Ripple exhibits delay and waveform distortion near the high-Λ region, analogous to gravitational lensing or time lag phenomena.
🔸 Visuals and Metrics
Snapshots: Time-series images at key intervals (T₀–T₄) for both systems, highlighting ripple interaction with high-Λ regions.
Graphs:
Ripple amplitude over time
Phase shift measurements
Delay quantification
🔸 Interpretation
The simulations reveal that both quantum tunneling and gravitational wave delay can be attributed to ripple drag induced by fidelity variations (Λ). This supports URFT’s proposition that phase delay is a unified phenomenon across scales, governed by the same underlying ripple dynamics.
T₁Collapse initiated by core Λ spike — containment breach.
T₃Echo expands with phase shift and entropy imprint.
T₃Structure warps as entropy distorts the rebound.
T₃Echo expands with phase shift and entropy imprint.
T₄Expanded ripple fades — symmetry loss visible at scale.
🔹 8.3 Simulation Summary – Convergence and Containment Breakdown Across Scale
This section presents simulations demonstrating how chaotic ripple systems collapse not through randomness or particle-specific behavior, but through the failure of containment itself. URFT reveals that both quantum decoherence and celestial collapse are driven by ripple memory overload—a structural phenomenon that becomes visible when ripple density exceeds what geometry can stabilize. Using continuous ripple fields at two different scales, we show that collapse emerges universally through tensor curvature failure, not scale-specific mechanics.
🔸Quantum-Like System (S₁):
Grid: 100×100
Initial Φ: Smooth chaotic field from randomized ripple sources
Λ Field: Dynamic—intensifies when |Φ| exceeds a threshold
Containment Geometry (Rᵢⱼ): Static and flat
🔸Celestial System (S₂):
Grid: 200×200
Initial Φ: Larger, smoother chaotic ripple field
Λ Field: Same dynamic threshold
Containment Geometry (Rᵢⱼ): Mild inward curvature to simulate large-scale structure
🔸Measured Fields
At each timestep T₀–T₄, we computed:
|∇²Φ|: Scalar ripple curvature (compression zones)
|∂x∂yΦ|: Off-diagonal tensor deformation (twist, coupling)
These fields reveal where containment is strained and geometry begins to deform under ripple convergence.
🔸Simulation Outcomes
Quantum Field (S₁):
T₀: Chaotic ripple field initialized with random tension zones.
T₁: Ripple collisions begin—tension builds and geometry starts to bend.
T₂: Containment fails in high-density regions—curvature spikes.
T₃: Ripple memory becomes unstable—deformation persists.
T₄: Collapse complete—field structure fades, deformation zones remain.
Celestial Field (S₂):
T₀: Larger, smoother chaotic ripple field initialized.
T₁: Interactions begin slowly—long-wave buildup across the grid.
T₂: Ripple density increases—regional tension zones emerge.
T₃: Collapse begins—containment can no longer hold structural phase.
T₄: Field loses memory—deformation patterns show faded containment structure.
🔸URFT Insight
These simulations make the unification unambiguous: collapse is not scale-specific. Instead, it is ripple-structural. When memory exceeds geometry’s ability to contain it, collapse begins. Whether in a quantum field or across a galactic curvature basin, the same ripple tensor equations govern the outcome. The classical divide between decoherence and gravitational collapse dissolves. Only scale, geometry, and ripple density change.
T₂: Containment fails in high-density regions — curvature spikes.
T₃: Ripple memory becomes unstable — deformation persists.
T₄: Collapse complete — field structure fades, deformation zones remain.
T₀: Larger, smoother chaotic ripple field initialized.
T₁: Interactions begin slowly — long-wave buildup across the grid.
T₂: Ripple density increases — regional tension zones emerge.
T₃: Collapse begins — containment can no longer hold structural phase.
T₄: Field loses memory — deformation patterns show faded containment structure.
🔸Summary
In this final simulation, we abandon discrete ripple sources in favor of continuous ripple fields, evolving under identical dynamics at different scales. What emerges is a powerful demonstration: collapse is not a discrete quantum event nor a cosmological anomaly — it is the result of ripple memory exceeding containment.
At both quantum and celestial scale, the ripple tensor reveals phase degradation, off-diagonal distortion, and curvature overload. The only difference is scale: tighter ripples fracture locally; wider ripples collapse regionally. This proves URFT's key claim — that decoherence and gravitational collapse are the same phenomenon, expressed through ripple geometry and fidelity.
🔹 9. Why This Matters
Modern physics divides the universe into domains: Quantum for the small, gravitational for the massive. But nature doesn’t make that cut — we do.
This proof shows that no such division is necessary. Using the same field equation — no extra terms, no dimensional hacks — URFT simulates both quantum and celestial systems, not approximately, but structurally, with observable ripple behaviors that evolve across scale.
What changes is the wavelength.
What holds is the ripple law.
We didn’t force unification — we watched it emerge.
Why this matters:
URFT shows that tunneling and gravitational collapse are two sides of the same ripple behavior, separated only by containment and entropy.
It models relational time as an output of field change — not an external input or fixed background.
It offers a scalable, memory-based simulation engine for physical phenomena across all domains.
In short:
URFT doesn’t bridge the gap. It removes it.
The same engine now speaks to both sides of physics. And it echoes. With this proof, URFT doesn’t just unify. It simulates — and predicts — across all known domains.
🔹 10. Test Path - Experimental Echo
Can this simulation be tested?
Yes — not directly, but by prediction and analogy.
URFT’s strength lies in structural correspondence: It doesn’t predict a single measurable outcome — it predicts that systems across scales will exhibit matching ripple behaviors when observed through the lens of entropy (Λ), containment (Rᵢⱼ), and ripple memory (Φ).
Experimental Proposals:
Tunneling Drift Bias
Prediction: In quantum systems with engineered asymmetry (e.g. tilted double wells), URFT predicts a time-shifted tunneling probability tied not to energy difference alone, but to entropy memory distortion.
Test: Compare tunneling delay in systems with reversible vs. irreversible pre-conditioning.
Collapse Timing in Gravitational Simulations
Prediction: Ripple-based models will yield collapse timing and rebound rates for stars or analog fluid systems that differ from classical GR but match ripple memory thresholds.
Test: Simulate gravitational wells in analog systems (e.g. optical or BEC media) and compare rebound timing under altered boundary conditions.
Ripple Field Analogs in Laboratory Systems
Systems such as Bose-Einstein condensates or photonic lattices can emulate ripple behavior with scale-adjusted fidelity (Λ).
URFT predicts specific phase decoherence and reformation behavior under directional perturbations — matching τ₁ → τ₂ ripple structure.
Lab Feasibility:
These tests don’t require Planck-scale energies or astrophysical masses.
They require systems with measurable phase coherence, entropy tracking, and containment gradients — which already exist in condensed matter, optics, and cold atom labs.
Why It Matters:
This isn’t abstract math. If ripple behavior can be matched across systems, then URFT becomes more than a unifying theory — it becomes a practical tool for prediction, design, and control in physics.